Свойства четырехугольников.
Свойства четырехугольников.
Основные формулы и свойства трапеции.
Основные формулы и свойства параллелограмма.
Основные формулы и свойства ромба.
Основные формулы и свойства прямоугольника.
Основные формулы и свойства квадрата.
Примеры и решения задач.
Разберем по сторонам каждый четырехугольник. А начнем с самой негармоничной фигуры — четырехугольника:

Выпуклым называется четырехугольник, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.
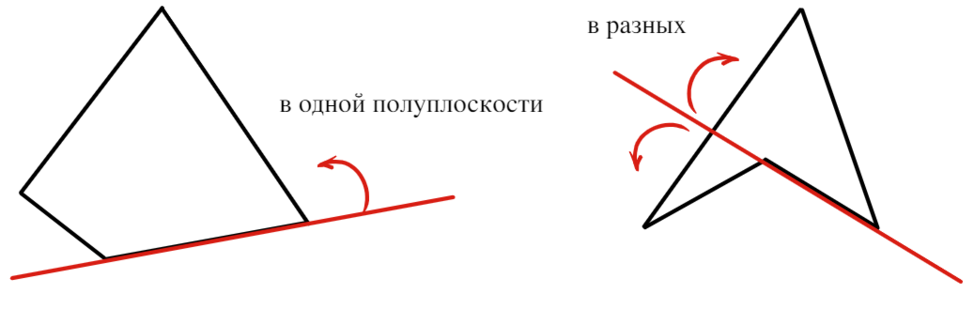
В ЕГЭ встречается только выпуклый, поэтому его брата оставим без внимания.
Если четырехугольник произвольный:
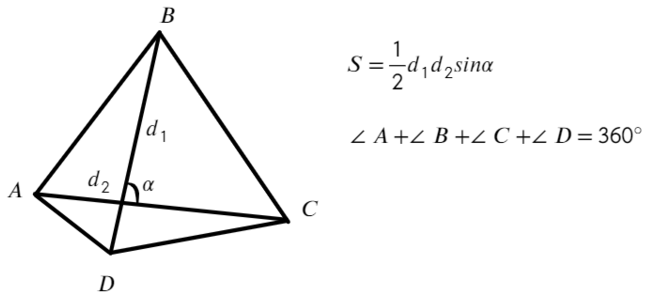
Если в четырехугольник можно вписать окружность, то помимо выше описанных свойств добавляются эти:
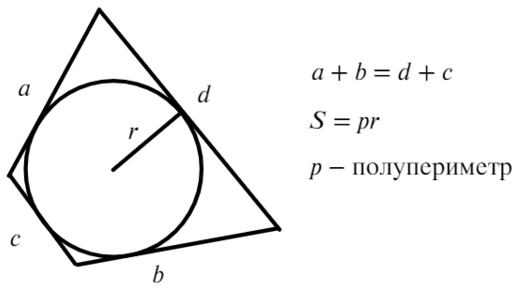
Если вокруг четырехугольника можно описать окружность, то добавляются такие свойства:

Две теоремы Птолемея можно встретить в №16 ЕГЭ, планиметрии повышенного уровня сложности.
Если поставить условие, что две противоположные стороны должны быть параллельны, то четырехугольник становится трапецией.
Всем привычна такая трапеция, но та, что справа, также существует!
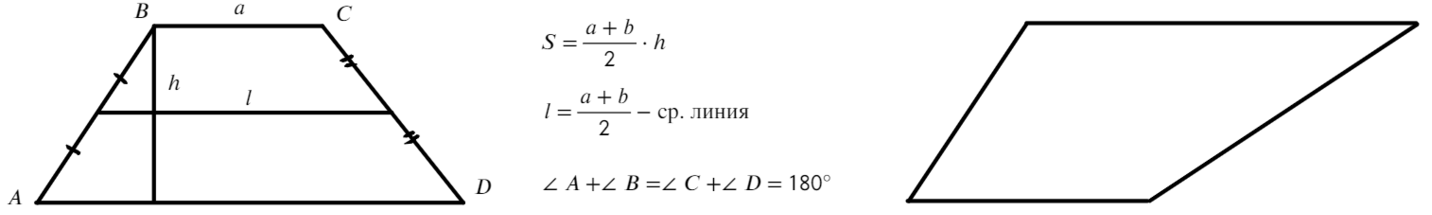
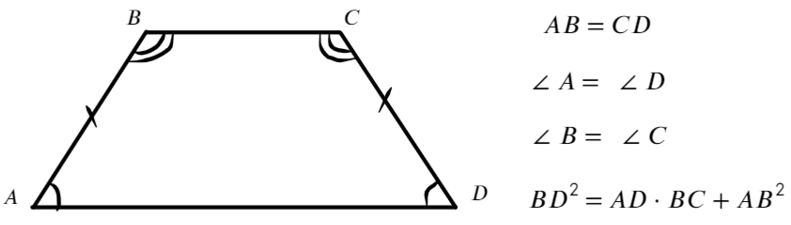
В равнобедренной трапеции:
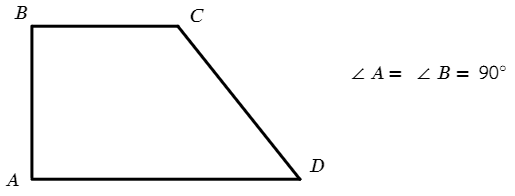
Прямоугольная трапеция:
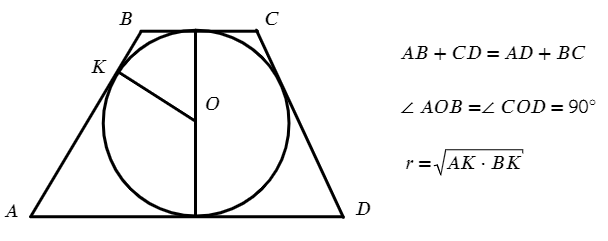
В трапецию можно вписать окружность, когда? Когда сумма противоположных сторон одинакова!
Да точно также, как и в четырехугольник, все свойства четырехугольника работают и в трапеции!
— И площадь через диагонали?
— Конечно!
А описать окружность вокруг трапеции? Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая!
Свойства остаются те же.
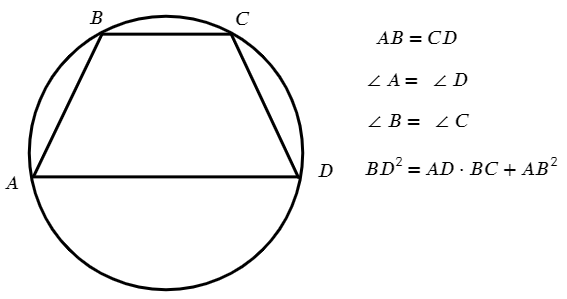
Следующий на очереди параллелограмм:
Если сказать, что в трапеции две попарно противоположные стороны параллельны, то трапеция станет параллелограммом.
Если сказать, что в трапеции две противоположные стороны параллельны и равны, то трапеция станет параллелограммом.
Еще добавляются 2 формулы площади:
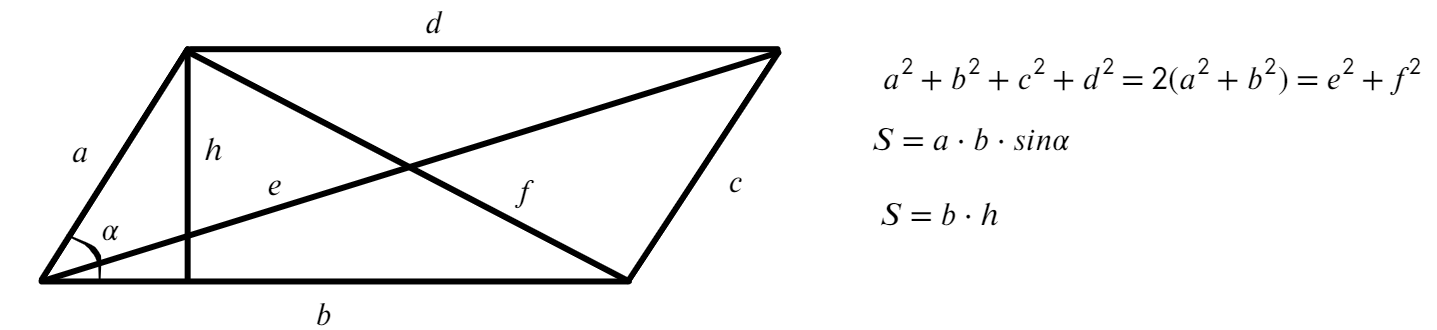
Свойства параллелограмма:
- Если у четырёхугольника противолежащие стороны попарно равны, то это параллелограмм.
- Если у четырёхугольника две противолежащие стороны равны и параллельны, то это параллелограмм.
- Четырёхугольник, диагонали которого в точке пересечения делятся пополам, – параллелограмм.
- Если у четырёхугольника противолежащие углы попарно равны, то это параллелограмм.
Дальше, чтобы из параллелограмма получить следующую фигуру, есть два пути:
1) Если у параллелограмма один угол 90°, то это прямоугольник.
2) Если у параллелограмма две прилежащие стороны равны, то это ромб.
Ромб — параллелограмм, у которого все стороны равны:
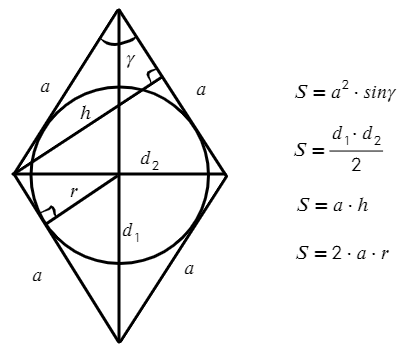
Свойства ромба:
- Диагонали ромба взаимно перпендикулярны.
- Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).
- Диагонали делят ромб на четыре равных прямоугольных треугольника.
- В ромб можно всегда вписать окружность.
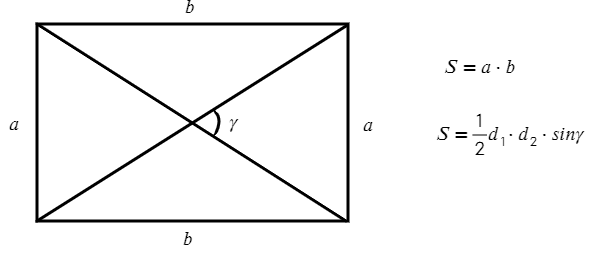
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Вокруг прямоугольника всегда можно описать окружность.
Правильный четырехугольник — квадрат. Папа был прямоугольником, а мама ромбом. Квадрат объединяет свойства и формулы этих фигур и добавляет свои:
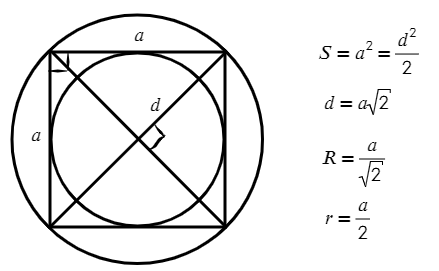
Свойства квадрата:
- Все углы квадрата прямые, все стороны квадрата равны.
- Диагонали квадрата равны и пересекаются под прямым углом.
- Диагонали квадрата делят его углы пополам.
- В квадрат можно всегда вписать окружность.
- Вокруг квадрата можно всегда описать окружность.
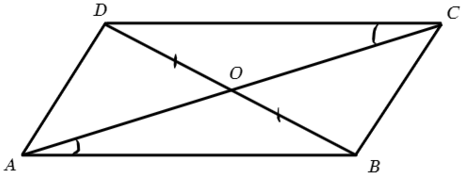
Задача №1 Докажите, что ABCD параллелограмм, если известно, что ∠CAD = ∠CAB и DO = OB.
Что нужно, чтобы сказать, что четырехугольник является параллелограммом?
- Две противоположные стороны параллельны и равны.
- Две попарно противоположные стороны параллельны.
Но раз DC II AB, то и ∠CDB = ∠DBA (как накрест лежащие), а ∠AOB и ∠DOC — рыжие что ли? Нет, они вертикальные, значит, тоже равны: ∠AOB = ∠DOC.
Тогда ΔAOB = ΔDOC (по стороне и двум прилежащим углам) => DC = AB.
Получается, что DC = AB и DC II AB, свойство №1 доказано.
Задача №2 Найдите периметр параллелограмма.
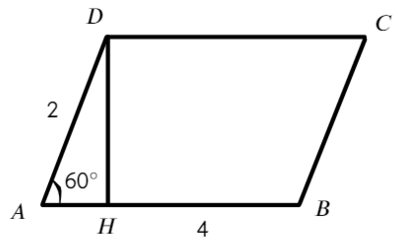
Вспомним, что в прямоугольном треугольнике находится против угла в 30°. Да-да, катет в два раза меньший гипотенузы. Следовательно AB = AH + HB = 1+4 = 5.
Тогда периметр:
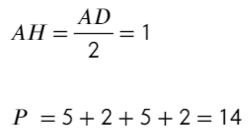
Ответ: 14.
Задача №3 Найдите площадь параллелограмма.
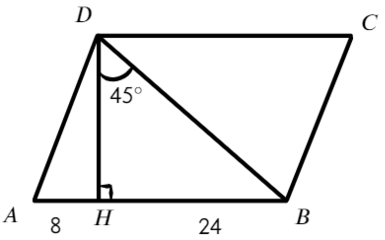
В ΔDHB ∠DBH = 180 – 90° – 45° = 45°=> ΔDHB — равнобедренный => DH = HB = 24
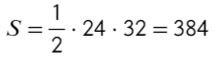
Ответ: 384
Задача №4 Найдите площадь ABCD.
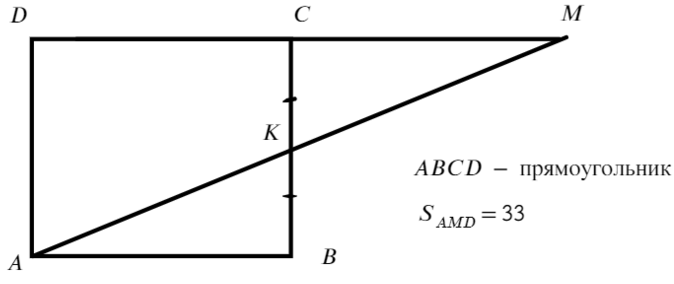
ABCD — прямоугольник. Чтобы найти его площадь, нужно знать две стороны, но мы знаем только площадь треугольника.

Площадь AKCD общая у ABCD и ADM, а вот отличаются они площадью ΔABK и ΔKCM, но мы только что доказали, что они равны, значит, площади ABCD и ADM тоже равны!
Ответ: 33
Задача №5 Найдите площадь трапеции, параллельные стороны которой равны 15 и 44, а непараллельные 17 и 25.
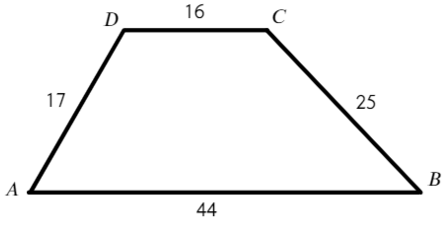
Площадь трапеции можно найти так:
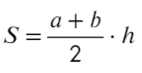
Не хватает высоты, попробуем разбить трапецию на треугольники и прямоугольник:
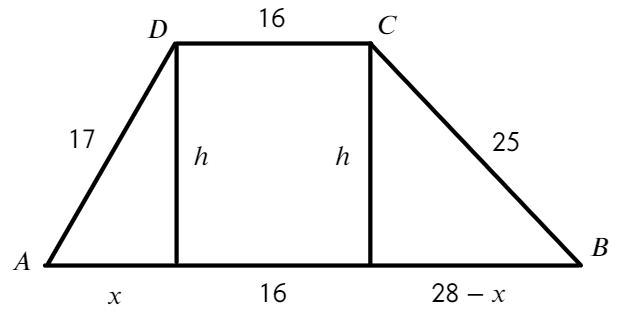
Запишем теорему Пифагора для двух треугольников:
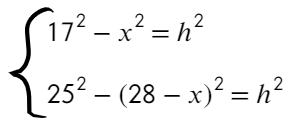
Решим уравнение:
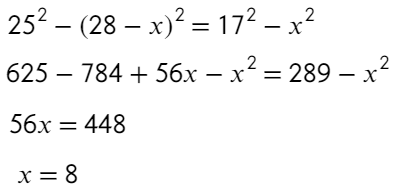
Зная, как разделится основание найдем высоту:
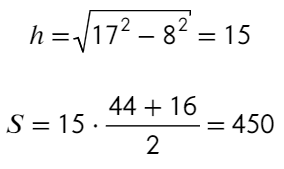
Ответ: 240
Задачи для закрепления с подсказками.
Если нашел опечатку, или что-то непонятно − напиши.