Вертикальные, смежные, соответственные, накрест лежащие углы.
Равенство и подобие треугольников.
Медиана, биссектриса, высота.
Свойства треугольников.
Площадь треугольников.
Кругом одна геометрия - круг друзей, квадрат врагов, треугольник любящих.
Ю. Татаркин
Давай на чистоту: геометрию трудно понимать, если не знаешь определенных теорем и свойств. Я постараюсь донести до тебя понятным языком только необходимое, а ты постарайся разобраться и запомнить!
Что такое луч, прямая, отрезок, угол, треугольник объяснять не буду, иначе кто-то уснет.
Когда небо было ярче, трава зеленее, а ты учился в 7 классе, началось знакомство с геометрией, туда и перенесёмся. Чтобы мы с тобой разговаривали на одном языке, начнем с равных углов.
Смежные углы — два угла, у которых одна сторона общая, а две другие расположены на одной прямой.
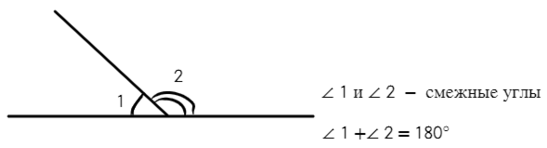
С вертикальными углами проще познакомиться на рисунке:
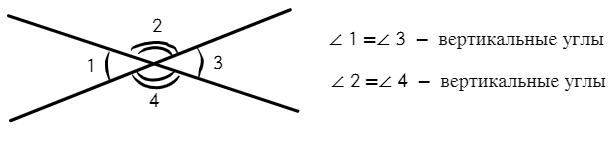
Такими дугами показываем равные углы ∠1 = ∠3 (одной дугой) и ∠2 = ∠4 (двумя дугами)
Теперь об углах при параллельных прямых (параллельные прямые — прямые, которые никогда не пересекутся, сколько бы их не продолжать. Лучше представить рельсы у путей на прямом участке):
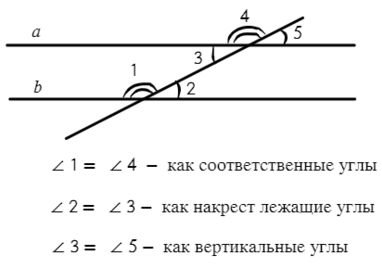
Перейдем к фигурам, а именно к равенству треугольников:
1) Треугольники, у которых две стороны и угол между ними соответственно равны двум сторонам и углу между ними другого треугольника, равны между собой.
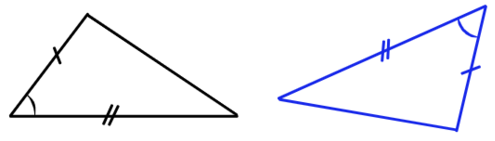
Штрихом и двумя штрихами показывают одинаковые стороны, которые равны между собой. Аналогично равные углы показывает одинаковым количеством дуг. Крайне удобно показывать дано сразу на рисунке.
2) Треугольники, у которых два угла и сторона между ними соответственно равны двум углам и стороне между ними другого треугольника, равны между собой.
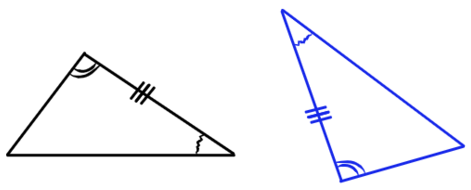
3) Треугольники, у которых три стороны соответственно равны трем сторонам другого треугольника, равны между собой.
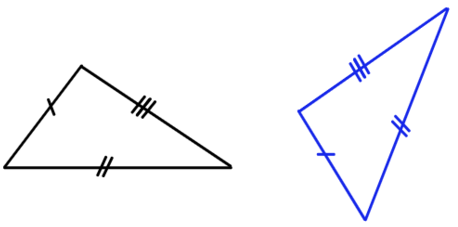
Одинаковые треугольники — это идентичные между собой фигуры, только развернутые. У тебя же не возникает вопроса, равны ли эти телефоны? Ты смотришь на форму, модель и сразу говоришь — идентичны. Так же поступай с треугольниками, только на слово тебе никто не поверит, обязательно нужно доказать один из трех признаков, описанных выше.
А вот эти фигуры какие?
Подобные! У них одинаковая форма, но разный размер. Тогда определим признаки подобных треугольников:
1) Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны.
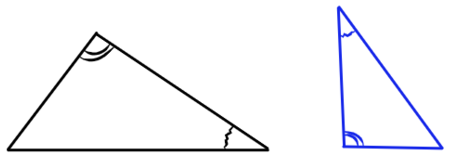
2) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
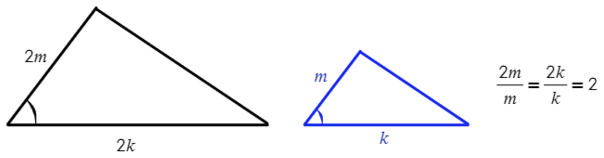
3) Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
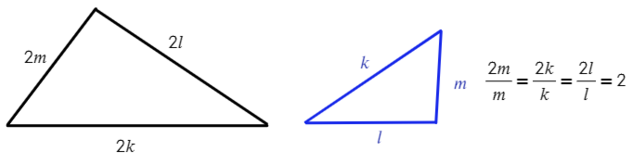
Важное свойство: если в подобных треугольниках отношение сторон равно k, тогда площади этих треугольников будут относится, как k² (покажу на примере задачи №7).
Давай закрепим теорию в задачах.
Введем секретный шифр:
«~» означает подобие
«Δ» означает треугольник
«∠» означает угол
Задача №1. Дано на рисунке:
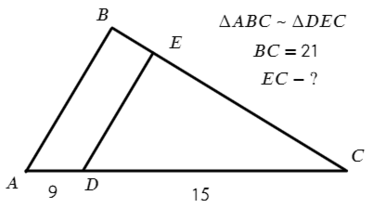
Т.к. треугольники подобны, запишем соотношения сторон против одинаковых углов.
AB II DE, значит ∠A = ∠EDC и ∠B = ∠DEC
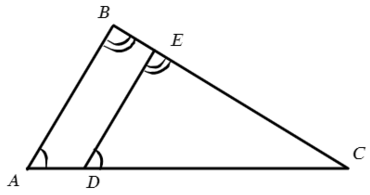
Запишем тогда отношение сторон и выразим нужную сторону EC:
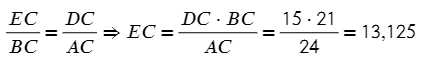
Ответ: 13,125
Задача №2. Дано на рисунке:
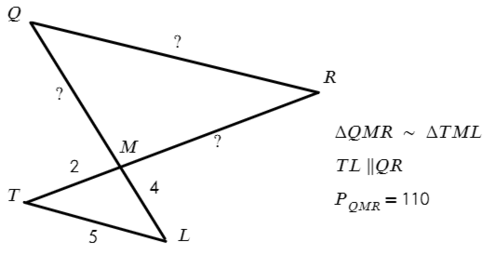
Периметр — это сумма всех сторон. Значит, если периметр отличается в 10 раз, то и стороны тоже в 10 раз.
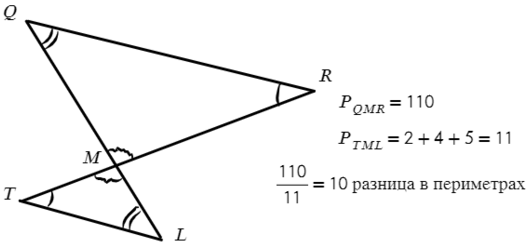
Но мы же знаем, что все стороны должны отличаться в 10 раз, тогда:
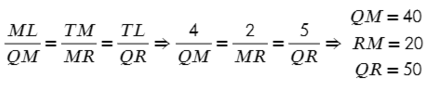
Ответ: 20; 40; 50.
Задача №3. Дано на рисунке:
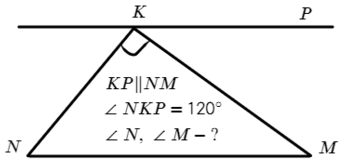
∠NKM = 90° и ∠NKP = 120°, значит ∠MKP = 30°
∠MKP = ∠KMN, как накрест лежащие углы при KP II NM => ∠KMN = 30°
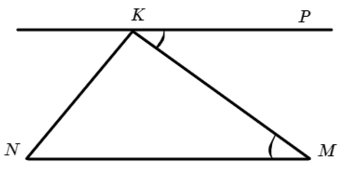
А сумма углов в треугольнике 180°, да-да, не всегда, конечно, но Неевклидовая геометрию оставим на другой раз.
∠KNM = 180 − ∠NKM − ∠KMN = 60°
Ответ: 60° и 30°
Теперь поговорим о самых распространенных отрезках в треугольнике: высота, биссектриса, медиана.
Высота — отрезок, опускающийся на прямую, содержащую противоположную сторону, под углом 90° (такой угол называется прямым).
Обратите внимание, что именно на прямую. В задаче №5 разберем почему.
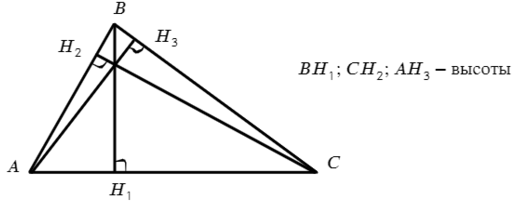
Угол 90° обозначается таким квадратиком у пересечения с прямой.
Биссектриса — луч, делящий угол, из которого выходит, пополам.
Запомнил, как обозначаем одинаковые углы? Одинаковым дугами.
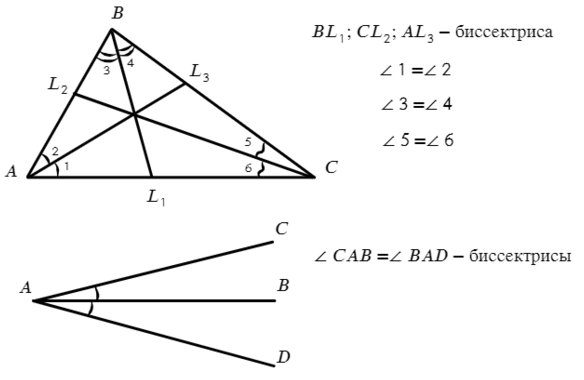
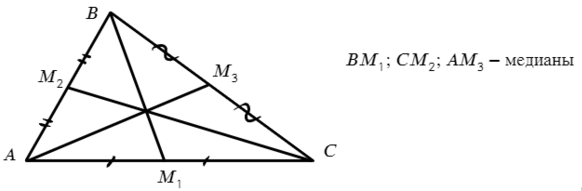
Медиана — отрезок, опускающийся из вершины треугольника на середину противоположной стороны.
Задача №4. Дано на рисунке:
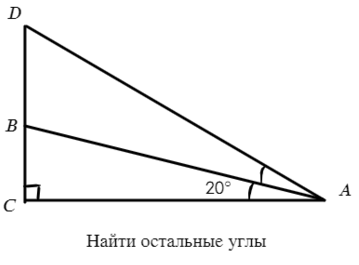
Давай посмотрим, что такое AB? АВ делит угол пополам (одинаковые дуги), значит, это биссектриса => ∠BAD = 20° => ∠CAD = 40°
В Δ CAD: ∠D = 180°− ∠C − ∠CAD = 50°, тогда
В Δ ВAD: ∠DBA = 180° − ∠D − ∠ВAD = 180° − 50° − 20° = 110°
∠DBA и ∠ABC — смежные (их сумма 180°) => ∠ABC = 180° − 110° = 70°
Задача №5. В ΔABC ∠B = 120°; ∠C = 30°. Из вершины А проведена высота, чему равен угол ∠BAH и ∠BAС?
Хороший рисунок — это 50% успеха, а в этой задаче все 90%. Рисуем треугольник примерно с углом 120°:
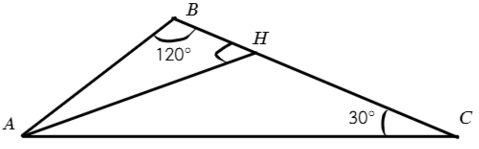
Рисунок получился плохой, а еще проблемы в ΔABH. Сумма углов должна быть 180°, но ∠B = 120° и ∠AHB = 90°, уже 210°! Что-то не так, вернемся к определению высоты — отрезок, опускающийся на прямую, содержащую противоположную сторону, под углом 90°.
Тогда продлим сторону BC, а на нее опустим высоту. Высота получится вне треугольника:
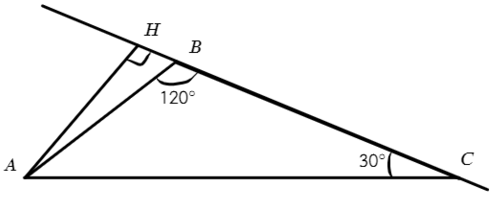
В ΔBAH: ∠HBA = 60° (смежный с ∠ABC) => ∠BAH = 180° − 60° − 90° = 30°
В ΔABC: ∠BAC = 180° − 120° − 30° = 30°
Ответ: 30° и 30°
Получается, что ∠BAC = ∠C = 30°, значит, этот треугольник равнобедренный. А что это такое?
Равнобедренный треугольник — треугольник, у которого две стороны одинаковой длины. Такие стороны называют боковыми, а сторону, которая им не равна, основанием.
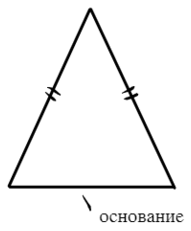Есть пара крайне полезных свойств в равнобедренном треугольнике:
1) Углы при основании равнобедренного треугольника равны.
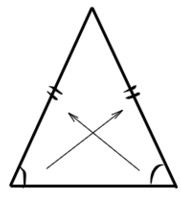
Против равных сторон лежат равные углы. Верно и обратное: если два угла у треугольника равны, то он равнобедренный
2) Медиана, проведенная к основанию треугольника, также является биссектрисой и высотой.
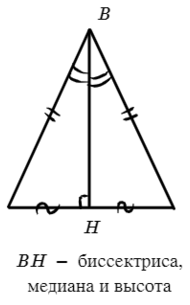
А что будет, если еще и третья сторона получится той же длины? Тогда этот треугольник равносторонний или правильный.
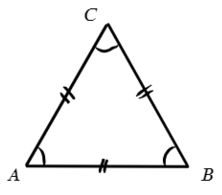
А чему равен каждый угол в равностороннем треугольнике? Сумма 180°, но все углы равны, они лежат против одинаковых сторон. Значит, один угол будет равен 180°/3 = 60°
А есть еще какие-то треугольники? Есть прямоугольный.
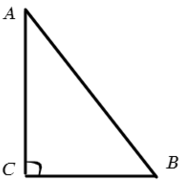
Прямоугольный треугольник — треугольник, у которого один угол равен 90° (прямой угол).
А два угла в треугольнике могут быть по 90°? Нет, тогда третьему углу останется 0°, нарисуешь такой?
Полезные свойства:
1) Катет, лежащий против угла в 30°, равен половине гипотенузы.
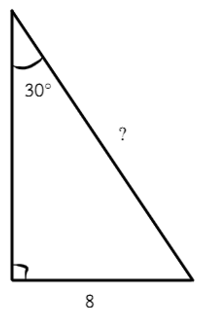
Гипотенуза будет в два раза больше катета и равна 16.
2) Медиана, проведенная из прямого угла, равна половине гипотенузы.
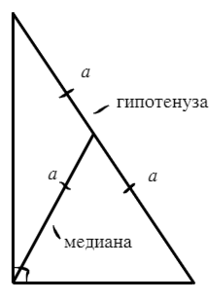
3) Теорема Пифагора
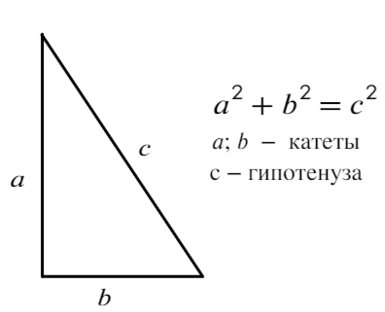
Теорема, которая встречается в 60% задач, а если дан прямоугольный треугольник — в 90%.
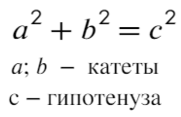
Квадрат гипотенузы (стороны против угла в 90°) равен сумме квадратов катетов.
Теорема Пифагора — это частный случай теоремы косинусов, но о ней мы потом поговорим.
Задача №6. Дано на рисунке:
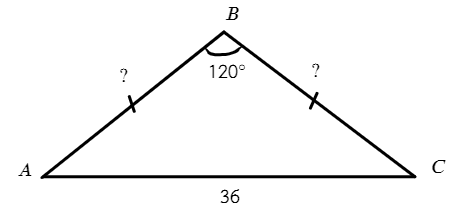
В ΔABC равнобедренный: ∠BAC = ∠BCA = 30°
Опустим высоту из вершины В:
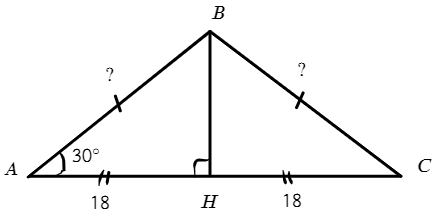
В равнобедренном треугольнике высота так же будет являться биссектрисой и высотой, значит AH = 18.
В ΔABH ∠A = 30°, скажем что BH = a, тогда AB = 2a. (против угла в 30° лежит катет в два раза больше гипотенузы)
В ΔABH по т. Пифагора:
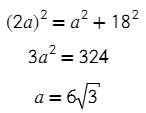
Ответ: 6√3.
Задача №7. ΔMNK ∼ ΔM₁N₁K₁. Площадь ΔMNK = 75, а площадь ΔM₁N₁K₁ = 225. Стороны соотносятся по названию. M₁N₁ = 9, чему равна MN
Вспомним про коэффициент подобия в площадях треугольника: если в подобных треугольниках отношение сторон равно k, тогда площади этих треугольников будут относится, как k²:
225/75 = 3 = k² => k = √3
M₁N₁/MN = k => MN = M₁N₁/k = 9/√3 = 3√3
Ответ: 3√3
Отлично, поздравляю тебя с Beginnerом по геометрии.
Вторая часть по треугольникам − площадь треугольников, свойства треугольников, тригонометрия в прямоугольных треугольниках, что такое синус/косинус, таблицы Брадиса (как пользоваться), теорема синусов и косинусов
Если нашел опечатку, или что-то непонятно − напиши.