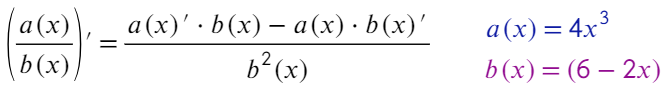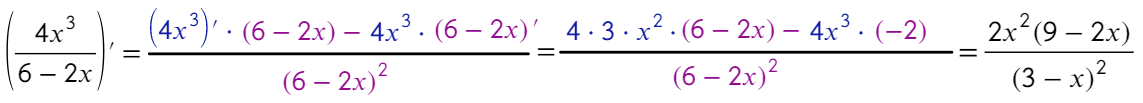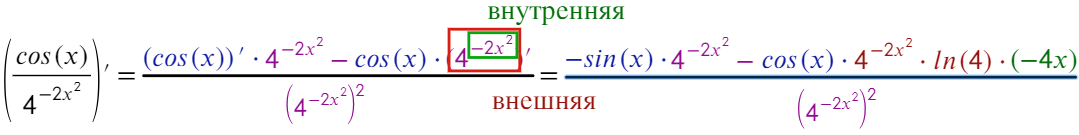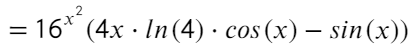Производная константы
Таблица производных
Сложные производные
Производная произведения
Производная частного
Надеюсь, ты уже понял, что такое производная? Для решения это, конечно, не критично, но для понимания важно!
Для обозначение производных ставят такой знак, который уже знаком из иностранных языков: «’» (апостроф).
Например: (xⁿ)' = nxⁿ⁻¹, то есть производная от xⁿ будет равна nxⁿ⁻¹.
Для нахождения производных выведен базовый набор формул, который нам сейчас пригодится!
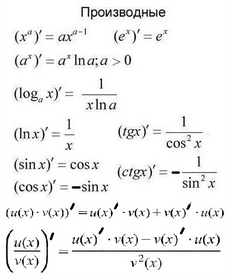
Самый большой секрет заключается в том, что производная от любого числа равна нулю.
(5)' = 0
(12646)' = 0
А производная от (π)' чему равна? Тоже ноль, это ведь тоже число!
Теперь c неизвестными:
(x)' = (x¹)' — если не указана степень у значения, то это число в первой степени (5 = 5¹).
(x¹)'? Для этого посмотрим на первую формулу ((xⁿ)' = nxⁿ⁻¹), где х — неизвестное, n — какое-то число.
Нужно значение в степени (сверху) поставить перед (умножить на) х, а показатель степени уменьшить на единицу!
В нашем случае (x¹)' => x = x; n = 1.
Тогда, подставив в формулу, получим: (x¹)' = 1x¹⁻¹ = 1x⁰ = 1×1 = 1 (Еще одна тайна: любое значение в нулевой степени равняется единице!).
(16x)' = (16x¹)' = 16×1×x¹⁻¹ = 16.
(0,5×x²)' = 0,5×2×x²⁻¹ = 1×x¹ = x.
Число перед иксом всегда остается перед значением! (В данном случае оставляем 16 и 0,5)
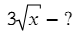
(корень без дополнительных обозначений говорит, что х находится в степени ½)
Та же перенесем ½ к 3-ке, а показатель степени уменьшим на единицу:
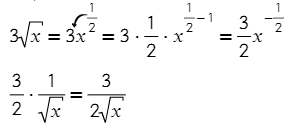
Последний пример на эту тему:
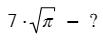
Пример кажется очень похожим на предыдущий, вот только где здесь x?
√π — хоть сразу и не скажешь, чему равняется это значение, но калькулятор знает! Значит, это число.
А производная от числа — это ноль!
Аналогично, используя формулы, можно брать производные от других функций:
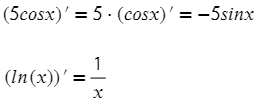
А как же обстоят дела с суммой и разностью производных? Берем производную от каждого члена, оставляя тот же знак:
(3x² − 2x + 1)' = (3x²)' − (2x)' + (1)' = 6x − 2 + 0 = 6x − 2.
(6x³ − 777)' = (6x³)' − (777)' = 18x² − 0 = 18x².
(2x⁷ + 5×е)' = (2x⁷)' + (5×e)'= 14x⁶ + 0 = 14x⁶ (e = 2,71828, значит, производная равна 0).
(2x⁻²)' = 2 × (-2) × x⁻³ = 4x⁻³.
(8sin(x) + 4ln(x) + 14x⁻²)' = 8cos(x) + 4/x + 14×(-2)×x⁻³ = 8cos(x) + 4/x − 28×x⁻³.
Кажется, ничего трудного нет, однако, если поставить цифру не перед функцией, а в нее, появятся сложности, о которых многие забывают:
((4x − 1)²)' − ?
Для начала пойдем простым путем: раскроем квадрат по определению и возьмем производную от каждого члена:
((4x − 1)²)' = (16x² − 8x + 1)' = (16x²)' − (8x)' + (1)' = 32x − 8.
Если теперь взять производную, как мы делали ранее: перенести 2-ку перед скобкой и уменьшить степень на единицу:
((4x − 1)²)' = 2×(4x − 1)¹ = 8x − 2. Не сходится!
Дело в том, что здесь уже появляются внешняя и внутренняя функции (это самое трудное в теме производных).
В таком случае берем производную сначала от внешней функции и умножаем результат на производную внутренней:
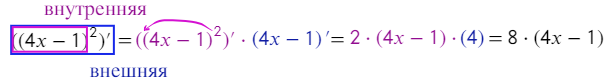
(ln(3x))' − ?
В данном случае есть внешняя функция «ln(3x)» и внутренняя функция «3x».
Еще одно важное замечание: у производной ln(3x) значение под логарифмом а = 3х, поэтому в знаменателе так же будет 3х!
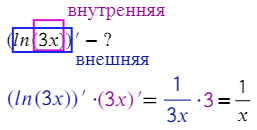
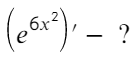
Самое главное определиться где внешняя, а где внутренняя функция.
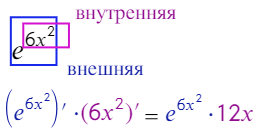
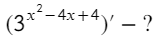
Это выражение относится к третьей формуле, а не к первой! Икс в данном случае находится в показателе степени (сверху), а основание (снизу) является числом (а = 3; х = x² − 4x + 4).
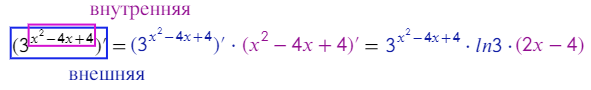
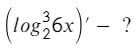
Здесь придется брать прозводную от степени, от логарифма и от значения под логарифмом или нет?
Упростить этот пример нам поможет свойство логарифма:
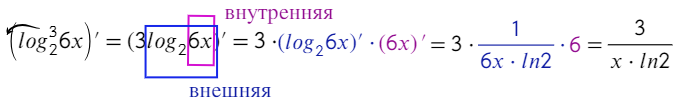
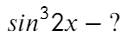
А вот этот пример уже трудно упростить, раскрытие синуса двойного угла только удлинит решение. Здесь нужно взять три производные: 1) от степени 2) от синуса 3) от значения под синусом.
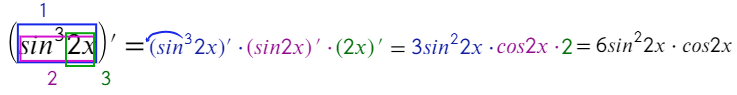
В сложных производных чаще всего (исключение составляет показательная функция, когда икс в степени) первую производную нужно брать от степени (² ³ ⁴ ⁵ ⁶), вторую от функции (ln; log; sin; cos), третью от значения под функцией (sin(3x); ln(14x²)).
С вычитанием и сложением мы разобрались, значит осталось?..
Для произведения и частного есть формулы (последние в табличке), которые стоит рассмотреть внимательнее.
Для произведения: производную первого множителя нужно умножить на просто второй множитель, плюс производную второго множителя умножить на первый.
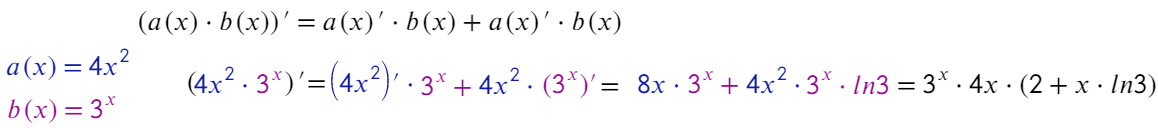
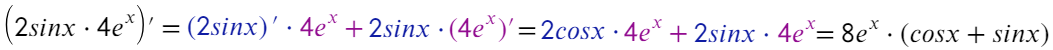
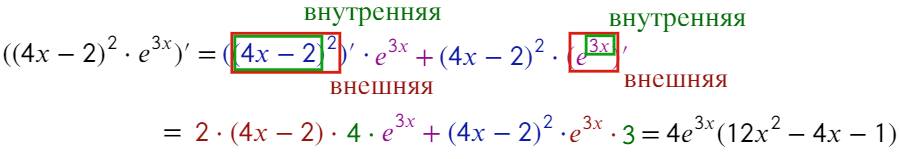

Для частного: производную числителя умножаем на знаменатель и вычитаем производную знаменателя, умноженную на числитель, и все вот это делим на квадрат знаменателя.