Производная по-простому
Где применяется
Немного о твоей будущей зарплате
Попробую объяснить несколько иначе, чем в школе.
Вы заканчиваете школу, поступаете в университет и начинаете подрабатывать:
В первый год после школы вы зарабатываете 0,5 у.е. (условных единиц).
Вы хорошо учитесь, устраиваетесь по специальности или находите свое призвание, и ваши дела постепенно, но идут в гору!
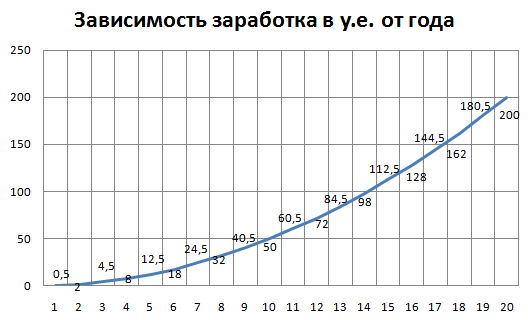
Какой молодец! Заработок растет не по годам, а по часам!
Если посмотреть на этот график внимательнее, то можно увидеть сходство с ветвью параболлы, которая в самом простом случае задается уравнением y = x². Если это понятно, то дальше все проще!
Интересно, а на сколько увеличивался заработок из года в год:
I год: 0,5 − 0 = 0,5 .
II год: 2 − 0,5 = 1,5.
III год: 4,5 − 2 = 2,5.
IV год: 8 − 4,5 = 3,5.
...
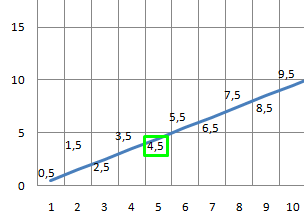
Получается, что наш доход каждый год возрастал равномерно. Вот что выйдет, если построить график:
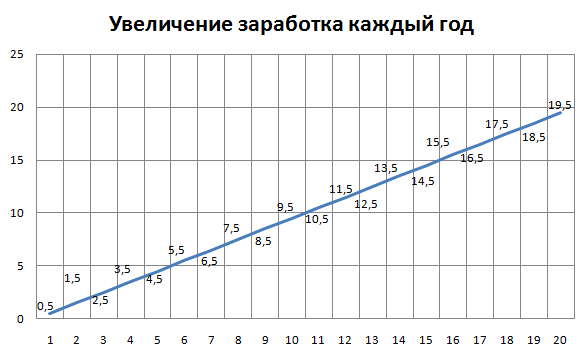
Получается прямая!
То есть все наши старания каждый год были постоянными, достаточно было ежегодно улучшать свой доход на 1 у.е.
Нетрудно заметить, что график заработка задается уравнением y = 0,5x².
А график увеличения заработка залается прямой y = x − 0,5.
Кто знает толк в производных, скажет «Неверно!». Конечно, производная от 0,5x² не будет равна x − 0,5, и это мы обсудим ближе к концу статьи.
Изменение заработка для нескольких лет
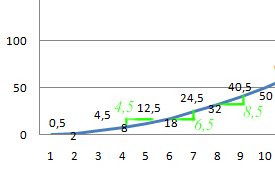
Для того, чтобы посчитать скорость изменения заработка, нужно взять один из «треугольников» с графика, например первый, и разделить длину вертикального катета (Δy) (в данном случае это 12,5 − 8 = 4,5) на длину горизонтального (Δx) (тут он равен 1).
Получится 4,5 / 1 = 4,5.
Таким образом, разделив вертикальный катет на горизонтальный, мы получаем скорость изменения функции, что показывает второй график.
Но как же это все относится к производным?
А так, что производная показывает «скорость» изменения функции!
Функция заработка предсталяет из себя график параболы (график функции) .
В тоже время функция увеличения заработка каждый год представляет прямую (график производной функции).
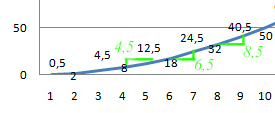
Однако прежде, чем ты расскажешь это своим друзьям, давай проверим, а если мы возьмем другой треугольник (в этот раз второй).
Вертикальный катет: 24,5 − 18 = 6,5.
Горизонтальный катет: 1.
Разделим: 6,5 / 1 = 6,5 — не сходится с первым треугольником!
А если объединить второй и третий треугольник?
Вертикальный катет: 40,5 − 18 = 22,5.
Горизонтальный катет: 9 − 6 = 3.
Разделим: 22,5 / 3 = 7,5 — опять не сходится!
Какая же тогда производная правильная?
Для того, чтобы верно найти производную, нужно взять как можно меньший горизонтальный катет - максимальное приближение (Δх)!
Сам график задается уравнением y = 0,5x².
Тогда возьмем x₁ = 4 => y₁ = 0,5 × 4² = 8, а при x₂ = 4,001 => y₂ = 0,5 × 4,001² ≈ 8,004.
Получается: Δy = 8,004 − 8 = 0,004, Δх= 4,001 − 4 = 0,001.
Производная: Δy / Δх = 0,004 / 0,001 = 4.
И что же тогда производная?
Производная — это скорость изменения функции при самых маленьких значениях Δх (наименьших значениях горизонтального катета).
Именно поэтому производную и называют тангенсом (отношение противолежащего катета к прилежащему) угла наклона этой функции.
Если же мы посчитаем производную для каждой точки, получится такой график функции:
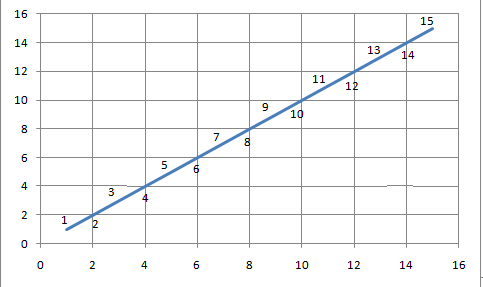
А это уже похоже на правду!
Производная от y = 0,5x² будет равна y = х (именно такой график получился у нас).

Погрешность в данном графике вызвана плохим приближением по оси х (в данном случае Δх = 1), из-за чего появляется неточность.
Конечно, можно не делать такое большое количество действий, проверяя точки.
Есть готовые формулы для базовых функций, пользуйтесь ими, если хотите облегчить себе жизнь.
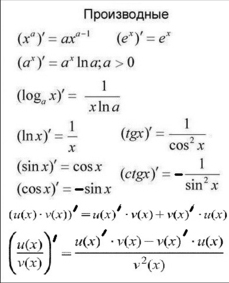
Выводы:
- Производные встречаются почти во всех областях: от медицины до финансов, по сути дела производная, показывая скорость изменения функции, предсказывает дальнейшее поведение функции.
- Представьте матрешку, так же как в каждой матрешке внутри есть следующая, так и функция скрывает в себе производную. У каждой функции есть своя производная функции. Так же можно брать от производной функции еще одну производную и повторять действие до бесконечности.
- Производная функции показывает скорость изменения самой функции. Так же, как у вас есть родители и предки (предыдущии поколения), которые вам передали какие-то отличительные особенности, так и у функции есть производная, которая передает ей скорость ее изменения.
Будь в курсе новых статеек, видео и легкого математического юмора.