Расстояние между точкой и плоскостью.

Расстояние между точкой и прямой.

Расстояние между двумя прямыми.

Первое, что полезно знать, это как найти расстояние от точки до плоскости: 

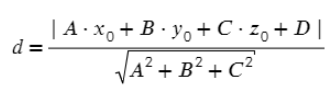
Значения A, B, C, D - коэффициенты плоскости

x, y, z - координаты точки

Задача. Найти расстояние между точкой А = (3; 7; −2) и плоскостью 4x + 3y + 13z - 20 = 0.

Все дано, можно сразу подставить значения в уравнение:

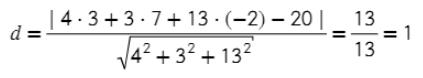
Задача. Найдите расстояние от точки К = (1; −2; 7) до прямой, проходящей через точки V = (8; 6; −13) и T = (−1; −6; 7).

1. Находим вектор прямой.
2. Вычисляем вектор, проходящий через искомую точку и любую точку на прямой. 
   
3. Задаем матрицу и находим определитель по двум полученным векторам в 1-ом и 2-ом пункте.
4. Расстояние получим, когда квадратный корень из суммы квадратов коэффициентов матрицы поделим на длину вектора, который задает прямую (Думаю непонятно, поэтому перейдем к конкретному примеру).

1) TV = (8−(−1); 6−(−6); -13-7) = (9; 12; −20)

2) Вектор найдем через точки K и T, хотя так же можно было бы через K и V или любую другую точку на данной прямой.

TK = (1−(−1); −2−(−6); 7-7) = (2; 4; 0)

3) Получится матрица без коэффициента D (здесь он не нужен для решения):

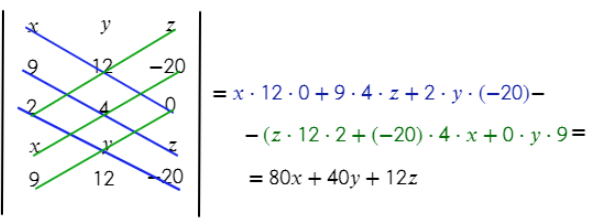Если непонятно, как получить матрицу и ее определитель, смотрите здесь более подробный разбор.

4) Плоскость получилась с коэффициентами А = 80, В = 40, С = 12,

x, y, z - координаты вектора прямой, в данном случае - вектор TV имеет координаты (9; 12; −20)

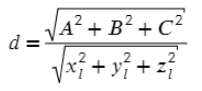
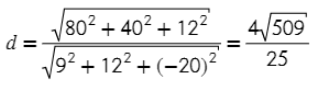
Задача. Найти расстояние между прямой, проходящей через точки Е = (1; 0; −2), G = (2; 2; −1), и прямой, проходящей через точки M = (4; −1; 4), L = (−2; 3; 0).

1. Задаем векторы обеих прямых.
2. Находим вектор, взяв по одной точке с каждой прямой.
3. Записываем матрицу из 3-х векторов (две строчки из 1-го пункта, одна строчка из 2-го) и находим ее численный определитель.
4. Задаем матрицу из двух первых векторов (в пункте 1). Первую строчку задаем как x, y, z.
5. Расстояние получим, когда разделим получившееся значение из пункта 3 по модулю на квадратный корень из суммы квадратов пункта 4. 

Перейдем к цифрам:

1) EG = (2−1; 2−0; −1−2) = (1; 2; −3)

ML = (−2−4; 3−(−1); 0−4) = (−6; 4; −4) 

2) Найдем вектор EM (можно было так же найти EL или GM, или GL).

EM = (1−4; 0−(−1); −2−4) = (−3; 1; −6)

3) Составляем матрицу из трех выше найденных векторов и находим определитель.

4) Составляем матрицу из первых двух выше найденных векторов и находим определитель 

без коэффициента D (здесь он не нужен для решения).

Вспомним, что уравнение плоскости задается так: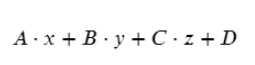

В нашем случае А = 4, В = 22, С = 16, D = 0.

5) Итоговая формула выглядит так, где L= −86 (из 3 пункта)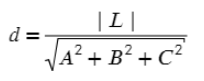

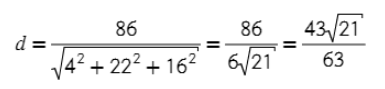
Будь в курсе новых статеек, видео и легкого математического юмора.