
Разбор самых нетривиальных задач с прикладным содержанием (подстановкой в формулу)
1) Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h(t) = -5t² + 18t (h - высота в метрах, t – время в секундах, прошедшее с момента броска). Найдите, сколько секунд камень находился на высоте не менее 9 метров.
Нарисуем данную ситуацию:
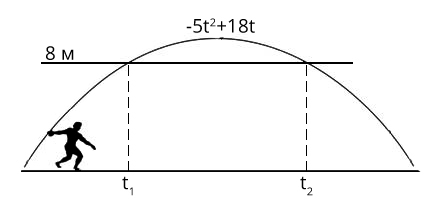
Полет камня задается уравнением: h = -5t² + 18t, то есть, подставив, например, вместо t ноль получим, что камень находился на высоте 0 метров. А в момент времени 3 секунды получим h = -5·3²+18·3 = 9 метров
Теперь, вспомнив 7-8 класс, когда мы строили графики и находили точку пересечения, сделаем здесь то же самое.
Приравняем -5t² + 18t = 9
После нескольких преобразований получим t = 0,6; t = 3 - абциссы точек пересечения двух графиков на рисунке (t₁ и t₂).
Ага, значит, камень находится выше 9 метров (параболла выше прямой) на промежутке от 0,6 секунды до 3 секунд.
Ответ: 2,4
2) Груз массой 0,7 кг колеблется на пружине. Его скорость υ меняется по закону υ = υ₀·sin(2·π·t /T) (*), где t — время с момента начала колебаний, T = 24 с — период колебаний, υ₀ = 0,6 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = m·υ²/2 (**), где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях.
Тут сразу две формулы! Давайте разбираться постепенно, нужно найти кинетическую энергию. Она выражена в (**) формуле, но чтобы ее найти, сначала нужно найти скорость в момент времени 10 секунд по (*) формуле.
Без ментальных знаний тригонометрии тут не обойтись, но мы попытаемся!
Подставим время и период в (*):
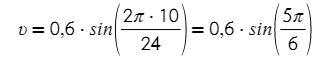
5·π/6 можно разложить как π-π/6, так ведь? 5/6 = 1-1/6
sin(π-π/6) можно разложить по формуле разности синуса или по формуле приведения
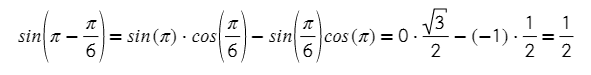
Получается, что υ = 0,6/2 = 0,3 м/с
Тогда энергия:
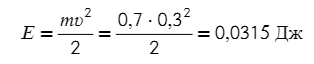
Ответ: 0,0315
3) Снаряд бросают под острым углом α к плоской горизонтальной поверхности земли. Максимальная высота полeта снаряда, выраженная в метрах, определяется формулой H=υ²·(1-cos2α)/4g, где υ = 22 м/с — начальная скорость, а g — ускорение свободного падения (считайте м/с). При каком наименьшем значении угла (в градусах) снаряд пролетит над стеной высотой 11,1 м на расстоянии 1 м?
Вопрос для правильного ответ: какая высота будет в формуле H?
Мячу нужно быть выше стены, которая высотой 11,1 метра, на 1 метр, тогда H = 12,1 метра, логично?
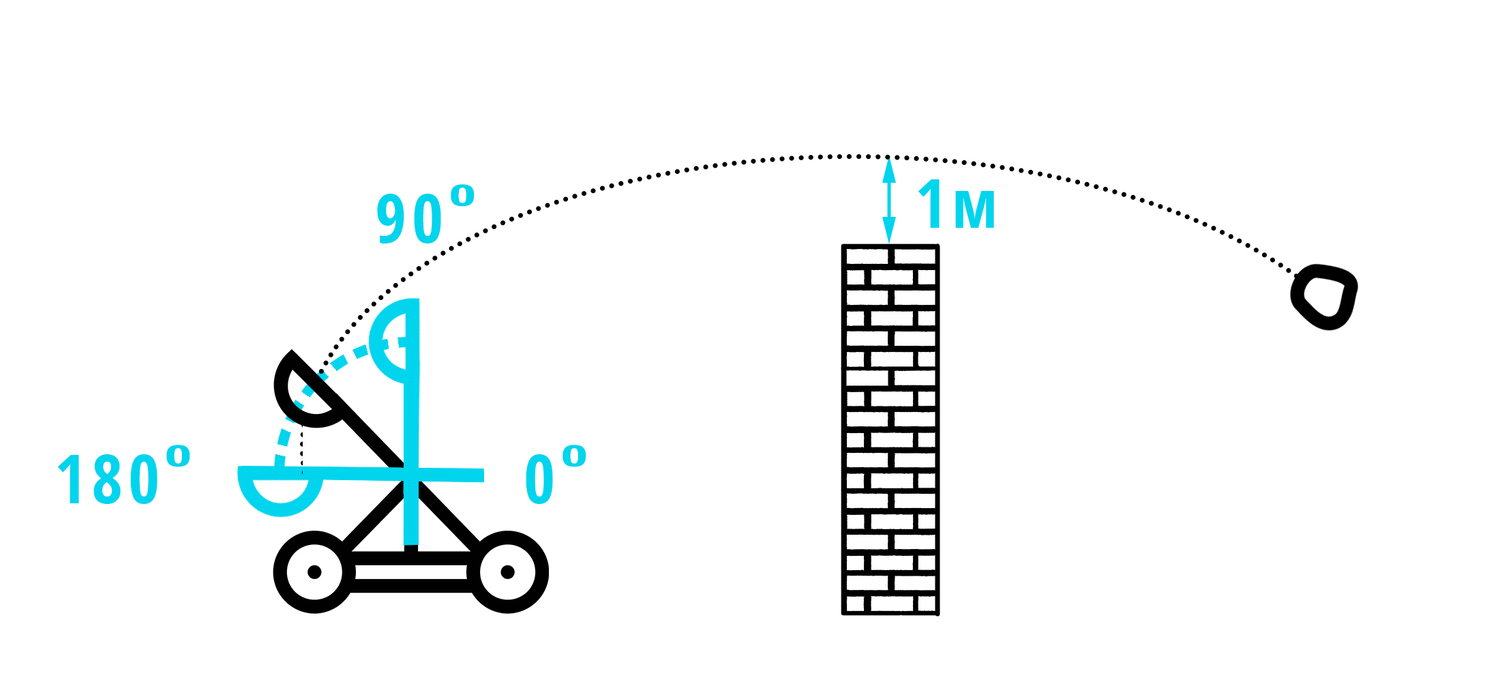
Все не так плохо, всего одна формула. Но нужно найти угол, и опять без тригонометрии не обойтись, но для начала выразим косинус:
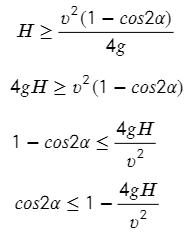
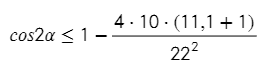
Угол у нас должен быть острый, то есть в промежутке от 0 до 90°, по-другому камень не перелетит через стену.
Косинус равен нулю, когда α = 90 для нашего случая.
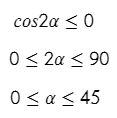
Угол нужен максимальный.
Ответ: 45
Теперь вы можете управлять осадой замка, а вдруг пригодится в XXI веке!
4) Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 50 см. Расстояние d₁ от линзы до лампочки может изменяться в пределах от 90 до 110 см, а d₂ расстояние от линзы до экрана — в пределах от 80 до 100 см. Изображение на экране будет четким, если выполнено соотношение 1/d₁+1/d₂=1/f. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
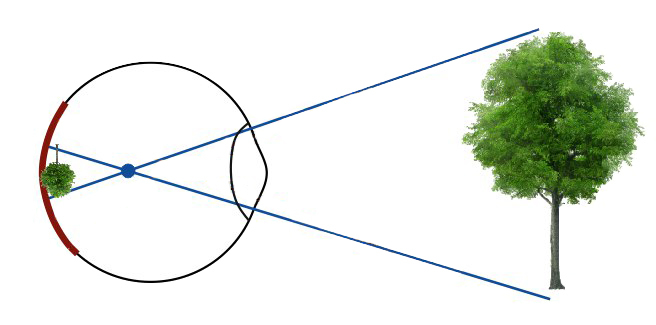
Одна из составляющих наших глаз - хрусталик, который представляет из себя собирающую линзу.
Наш глаз так же, как и линза, имеет расстояние, на котором он сможет сфокусироваться.
В задаче используется собирающая линза (это "двойной вектор" по середине). Фокусное расстояние обозначено f и показывает расстояние от линзы до точки фокусировки.
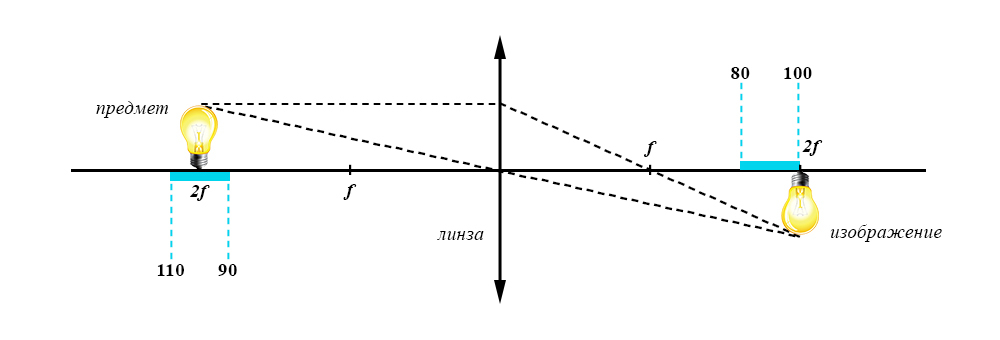
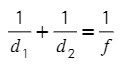
Требуется найти наименьшее расстояние от линзы до лампочки - d₁.
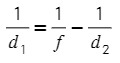
Если мы берем наименьшее d₁, тогда дробь 1/d₁ будет наибольшей (Сравните дроби 1/5 и 1/10, чем меньше знаменталь, тем больше будет дробь).
Получается, что разность тоже должна быть как можно больше (1/50-1/d₂).
Значение f постоянно, а вот d₂ мы вольны выбирать из диапазона. Тогда дробь 1/d₂ возьмем как можно меньше (чтобы 1/50-1/d₂ было как можно больше). Для этого d₂ возьмем как можно больше из заданного диапазона - 100 см.
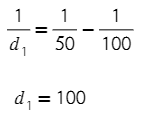
Данное значение попадает в диапазон. Изображение будет четким, а расстояние наименьшим.
Ответ: 100
5) Уравнение процесса, в котором участвовал газ, записывается в виде p·Vⁿ = const, где p (Па) — давление в газе, V — объeм газа в кубических метрах, n — положительная константа. При каком наименьшем значении константы n уменьшение в 9 раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 3 раза?
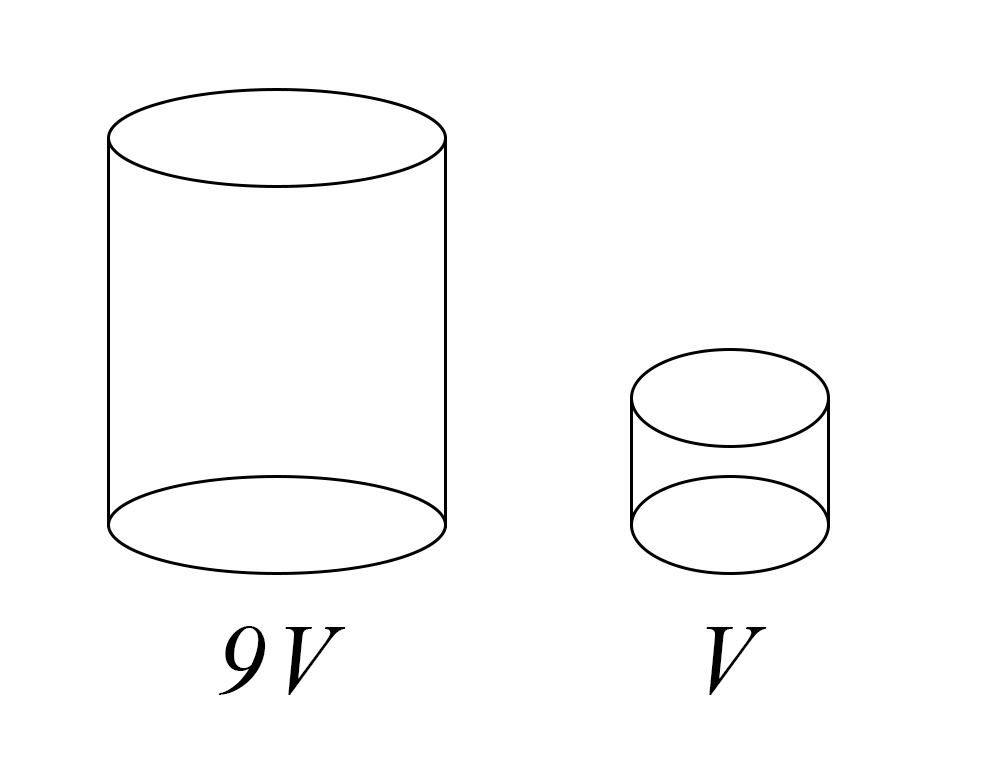
Начнем с интересного слова "const": оно означает, что данное выражение должно всегда оставаться постоянной (6·4, уменьшив 6 в 2 раза, а 4 увеличив в 2 раза получим 3·8 = 6·4). То же самое происходит здесь:
p₁·V₁ⁿ = p₂·V₂ⁿ
Сказано, что объем уменьшается в 9 раз, то есть начальный объем был V₁, а стал V₁/9.
Не нравятся неизвестные? Пусть V₁ = 1, тогда V₂ = 1/9 ( главное, чтобы разница был в 9 раз).
То же самое с давлением p₁ и 3p₁ (или p₁ = 1, тогда p₂ = 3).
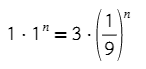
Единица в любой степени всегда останется единицей:
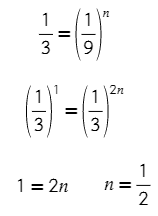
Ответ: 0,5
Будь в курсе новых статеек, видео и легкого математического юмора.