Что такое теорема о трех перпендикулярах простыми словами
Как ее использовать в задачах
Как оформлять на ЕГЭ
Начнем с парочки вводных понятий, ты же хочешь жить по понятиям?
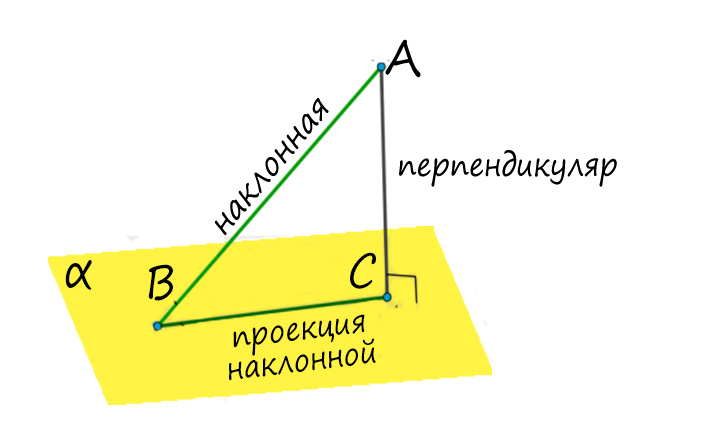
Если в плоскости альфа провести прямую KL через точку В так, что KL ⊥ BC, тогда по теореме о трех перпендикулярах (т.т.п.) KL ⊥ BA.
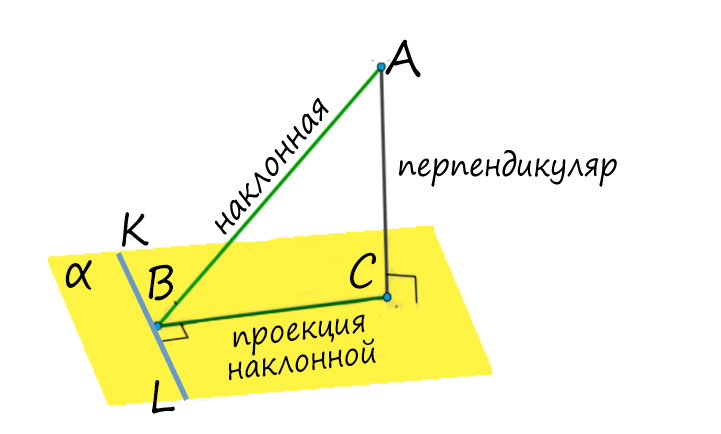
Словами можно сказать так: прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость (верно и наоборот).
Перейдем к самому распространенному примеру:
1) Докажите, что в тетраэдре скрещивающиеся ребра перпендикулярны.
У тетраэдра есть три пары скрещивающихся ребер. Докажем перпендикулярность одной пары, другие вы сделаете по аналогии, например, AD ⊥ BC.
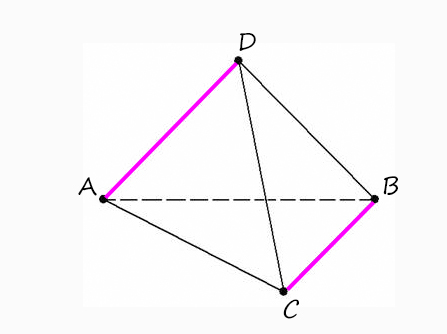
Сейчас есть только наклонная AD и плоскость (ABC), значит, нам не хватает проекции наклонной и перпендикуляра, тогда проведем их:
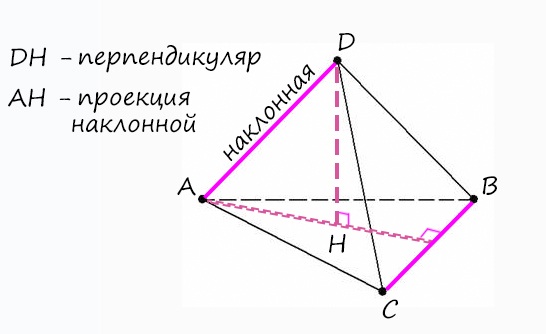
Тогда, чтобы доказать, что AD ⊥ BC:
1) AH ⊥ BC (если продлить АН до пересечения с BC), т.к. AH является выстой в правильном треугольнике.
2) DH ⊥ (ABC) (по построению, а, значит, перпендикулярно любой прямой, находящейся в этой плоскости) => DH ⊥ BC.
После того, как мы это доказали, можем смело сказать, что AD ⊥ BC (всегда дожно быть доказательство двух пунктов, и только тогда вывод).
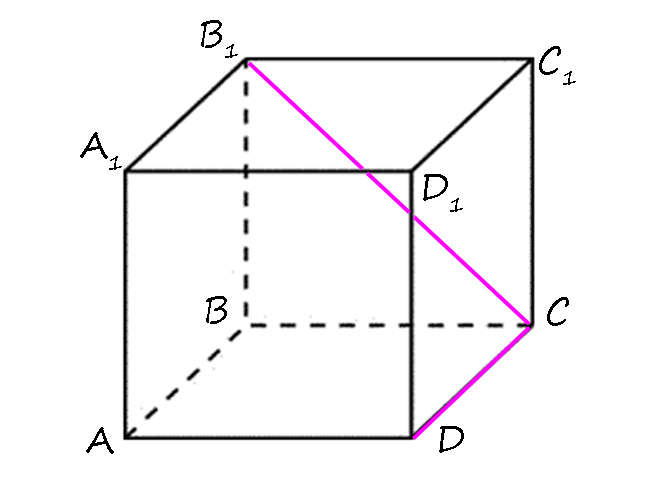
2) Докажите, что в прямом параллепипеде ребра B₁C и CD перпендикулярны.
Возьмем B₁C как наклонную к плоскости (ABCD), тогда перпендикуляром будет BB₁, а проекцией наклонной на эту плоскость — BC.
1) BB₁ ⊥ (ABCD) т.к. параллепипед прямой (боковые ребра перпендикулярны плоскости основания) => BB₁ ⊥ CD (если прямая перпендикулярна плоскости, то и перпендикулярна всем прямым, лежащим в этой плоскости).
2) BC ⊥ CD т.к. ABCD — прямоугольник.
3) По т.т.п.: B₁C ⊥ CD.
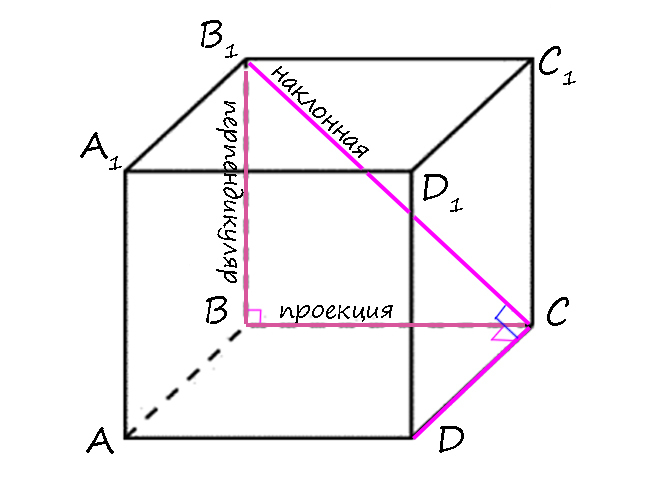
Два пункта доказательства, третий пункт вывод.
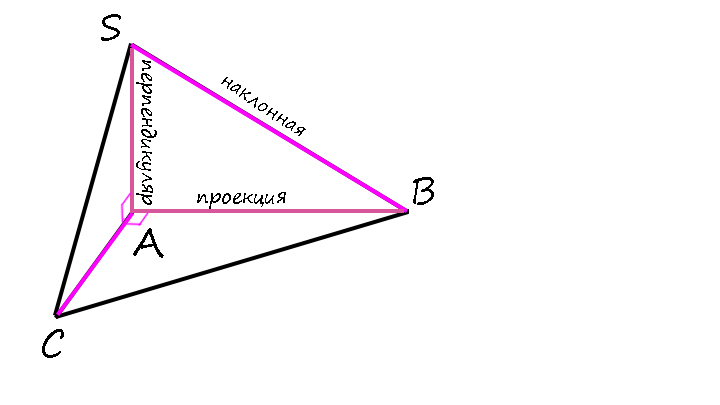
3) Дана пирамида SABC с высотой AS, в основании которой лежит прямоугольный треугольник с прямым углом A. Докажите, что SB⊥ AC.
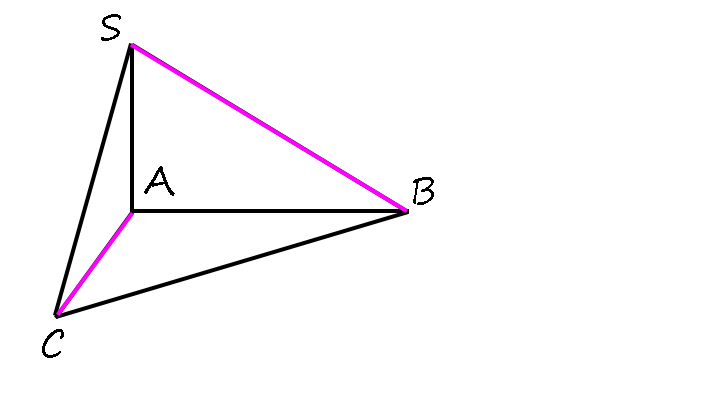
Скажем, что BC — наклонная к плоскости (ABC):
1) SA ⊥ (ABC) => SA ⊥ AC
2) AB ⊥ AC ( ABC — прямоугольный треугольник по условию).
3) По т.т.п.: SB ⊥ AC.
Вывод:
Два пункта доказательство и вывод!
1) Перпендикуляр будет опускаться на плоскость под 90°.
2) Проекция наклонной на плоскость перпендикулярна прямой.
3) По т.т.п. наклонная перпендикулярна прямой.