
Задачи с уравнением координат в первой части ЕГЭ.
На youtube'e можно найти много хороших видео-роликов про теорию на эту тему. Не хочу повторяться.
Если хотите посмотреть сразу решение конкретной задачи, то смело листайте до заданий.
Я лишь расскажу самую суть, которая потребуется в решении заданий на ЕГЭ.
Физический смысл производной:
Производная от уравнения координаты равна уравнению скорости.
Производная от уравнения скорости равна уравнению ускорения.
Предоположим, что нам нужно кинуть мячик, а компьютер записывает уравнение зависимости высоты полета от времени.
Как мы будем кидать? Конечно, немного вверх и вперед!
И вот, нам приносят распечатку уравнения траектории мячика:
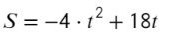
И как это использовать? А очень просто! Согласитесь, движение мячика — это параболла, ветви которой направлены вниз. Из уравнения можно найти корни: 0 секунд (где мы стояли) и 4,5 секунды (куда приземлился камень). Подставив вместо t любое значение, мы можем найти высоту, на которой находится мячик в момент времени t!
И тут нам сказали найти скорость мяча по вертикали через 2 секунды полета. Хм, вспомним, что там было написано в начале статьи. Ага! Производная от уравнения координаты — это уравнение скорости.
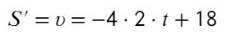
Подставив в уравнение вместо t = 2 секунды, получим:
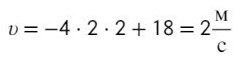
Можно найти скорость в любой момент времени, в том числе, когда она будет равна нулю.
А теперь задания из ЕГЭ:
Задание №1. Материальная точка движется прямолинейно по законум x(t) = − 0,5t² + 9t − 29 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени 7 с.
Возьмем производную от этого уравнения:
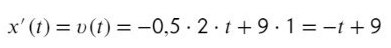
Осталось подставить вместо t = 7 секунд:
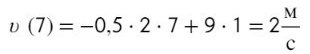
Задание №2. Материальная точка движется прямолинейно по закону x(t) = t² − 11t + 29 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Здесь необходимо решить обратную задачу: зная скорость, нужно найти время.
Возьмем производную:
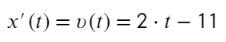
Приравняем к 3 м/с и найдем время:
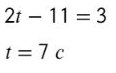
Задание №3. Материальная точка движется прямолинейно по закону x(t) = − 0,5t³ + 6t² − 4t −7 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 20 м/с?
Задание аналогичное предыдущему, производная только чуть труднее:
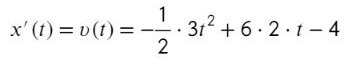
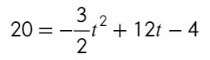
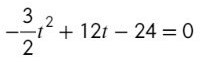
После некоторых манипуляций с дискриминантом или т. Виетта получаем, что t = 4 с.
Задание №4. Материальная точка движется от начального до конечного положения. На рисунке изображён график её движения. На оси абсцисс откладывается время в секундах, на оси ординат — расстояние от начального положения точки (в метрах). Найдите среднюю скорость движения точки. Ответ дайте в метрах в секунду.
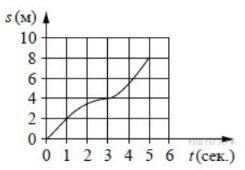
Все, что нужно вспомнить — это что такое средняя скорость? Это весь путь, деленный на все время. Поэтому 8 делим на 5 и получаем 1,6 м/с! Никакие производные здесь не требуются.
Будь в курсе новых статеек, видео и легкого математического юмора.