Пример решения задачи на движение по воде

Теп­ло­ход про­хо­дит по те­че­нию реки до пунк­та на­зна­че­ния 459 км и после сто­ян­ки воз­вра­ща­ет­ся в пункт от­прав­ле­ния. Най­ди­те ско­рость те­че­ния, если ско­рость теп­ло­хо­да в не­по­движ­ной воде равна 22 км/ч, сто­ян­ка длит­ся 10 часов, а в пункт от­прав­ле­ния теп­ло­ход воз­вра­ща­ет­ся через 54 часа после от­плы­тия из него. Ответ дайте в км/ч.

Разберем по пунктам:

1. Задачу прочитали.
2. Определяемся, про что задача: работа, движение, проценты? Движение.
3. Точные данные: расстояние между пунктами назначения 459 км = S. 
4. За X берем скорость течения.  Теперь стоит вернуться к пункту 4 и пояснить, чему равна скорость лодки. Скорость лодки по течению равна 22 + Х (Представим, что мы отправились на плоту и не прилагаем никаких усилий, плывем по течению - двигаемся со скоростью течения реки. Теперь, если мы начнем грести по направлению течения, наша скорость будет равна скорости течения плюс скорость, которую мы получаем от наших усилий - то есть наши усилия с рекой суммируются). Скорость лодки против течения 22 - Х (теперь мы преодалеваем усилия реки и движемся наперекор ей, для этого нам нужно затратить столько же скорости, сколько и реке).
5. Теперь выразим время (t) через скорость (v) и путь (s). Время = путь / скорость.

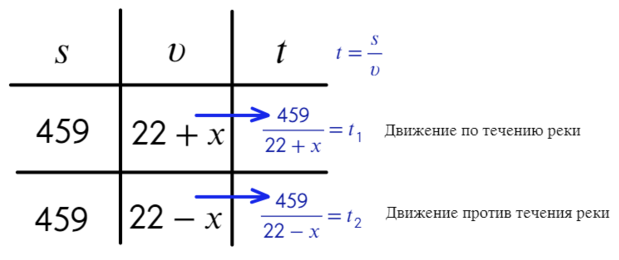
    6   Дополнительное условие: теплохода не было в пункте, из которого он выплыл 54 часа, из них он был на стоянке 10 часов, то есть его время в пути 54 - 10 = 44 часа = t. Это сумма времени по течению (t₁) и против (t₂).

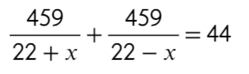
Решим это уравнение:

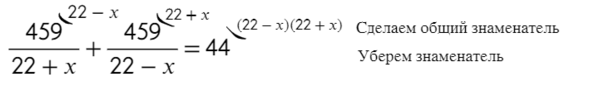
Так лихо убрать знаменатель можно в связи с тем, что скорость не может равняться 22, тогда скорость теплохода была бы равна скорости течения, и силушки у теплохода не хватило бы, чтобы идти против течения.

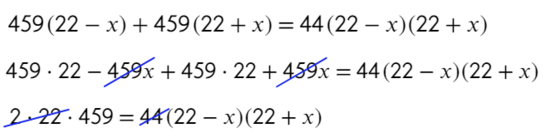
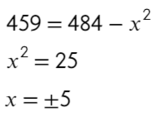
Ответ: 5.

Пример решения задачи на прямолинейное движение 

Два че­ло­ве­ка одновременно от­прав­ля­ют­ся из од­но­го дома до опуш­ки леса, на­хо­дя­щей­ся в 2,4 км. от дома. Один идёт со ско­ро­стью 3 км/ч, а дру­гой — со ско­ро­стью 4,2 км/ч. Дойдя до опуш­ки, вто­рой с той же ско­ро­стью воз­вра­ща­ет­ся об­рат­но. На каком рас­сто­я­нии от точки от­прав­ле­ния про­изойдёт их встре­ча? Ответ дайте в ки­ло­мет­рах.

1. Задачу прочитали. 
2. Определяемся, про что задача: работа, движение, проценты? Движение. 
3. Точные данные: скорость первого 3 км/ч, второго - 4,2 км/ч.
4. За Х берем расстояние от дома до места их встречи, то есть путь, который прошел первый человек. Второй двигается быстрее первого, то есть он первый дойдет до опушки леса и повернет обратно, пока первый человек будет двигаться к опушке.

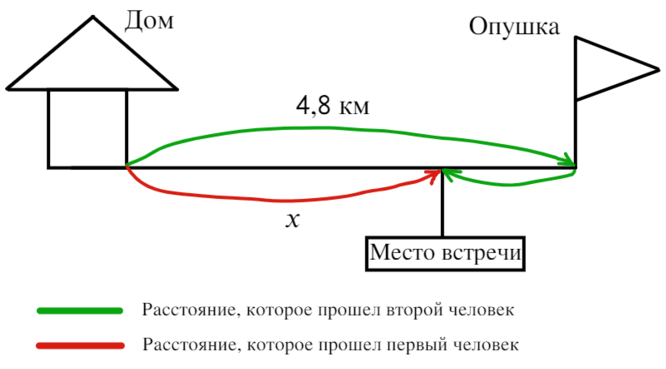
     5   Тогда путь, который прошел второй человек - это расстояние от дома до опушки (4,8 км) и путь от опушки до места встречи ((4,8 - Х) км) => Путь второго человека: 4,8 + 4,8 - Х = 9,6 - Х. Путь первого человека: Х.

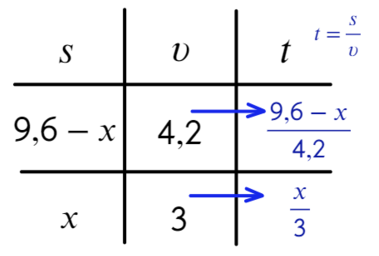
     Теперь выразим время (t) через скорость (v) и путь (s). Время = путь / скорость.

    6   Дополнительное условие: его тут нет. Все данные в задачке мы уже использовали. Тогда к чему же приравнять их время в движении? Ко времени друг друга. Вышли они одновременно, и все время, пока шел первый человек, шел и второй.

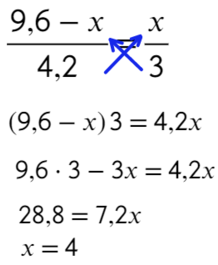
Пример решения задачи на движение по окружности

Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 40 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 25 км/ч больше скорости другого?

1. Условие прочитали. 
   
2. Определяемся, про что задача: работа, движение, проценты? Движение.
   
3. Точные данные: скорость одного на 25 км/ч больше чем у другого. (важно - стартовали мотоциклисты из двух диаметрально противоположных точек трассы, изначальное расстояние между ними 20 км). Сложность в этой задачи в том, что длину трассы пока не нужно использовать.
   
4. За t берем время, сколько им потребуется, чтобы встретиться. А за х скорость медленного мотоциклиста.
   
5. Выражаем путь (S) через время и скорость.
   
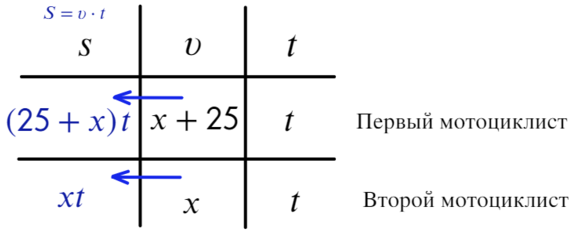
6. Еще никак не использовано расстояние между мотоциклистами - 20 км. Тогда путь, который проехал более быстрый до место их встречи минус путь, который проехал более медленный равно 20 км!

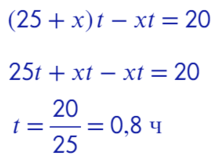
Ответ: 48.

Пример решения задачи на работу

Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?

1. Условие прочитали. 
2. Определяемся, про что задача: работа, движение, проценты? Работа. 
3. Точные данные: время первого 20 мин., второго 30 мин., третьего 60 мин. (важно - время каждого насоса выразить или в минутах, или в часах).
4. За Х берем время, за которое все три насоса наполнят бассейн.
   
5. Производительность P = A / t первого насоса - A/20, второго - A/30, третьего - A/60.

       Теперь выразим производительность (Р) через работу (A) и время (t). P = A / t

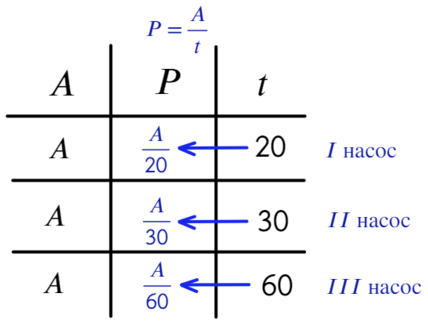
   6  Последнее действие: всю работу (А) разделим на сумму производительностей всех трех насосов и получим время, за которое все три насоса, работая вместе, наполняют бак.

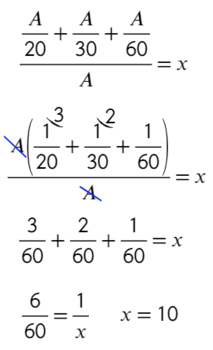
Проверьте себя на глупость: 3 насоса должны наполнить бак быстрее, чем каждый по отдельности.

Ответ: 10.

Пример решения задачи на проценты

В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

1. Задачу прочитали.
2. Определяемся, про что задача: работа, движение, проценты? Проценты. 
3. Точные данные: объем первого расствора до добавления воды - 5 литров, после - 5 + 7 = 12 литров (в формуле говорится о массе, но эта формула так же справедлива и для объемов, то есть весь объем жидкости умножить на процент равняется объему какого-то вещества), тогда раз у нас изменения происходят после добавления воды, возьмем первую строку - до добавления воды, вторую - после добавления воды.
4. За Х берем процент после добавления воды. 
5. Объем активного вещества найдем как произведение всего объема жидкости на процент (Почему так? - В аптеке продается медицинский спирт, на котором написано содержание спирта 95% и воды 5%,  допустим, объем его 1 литр, тогда объем чистого спирта составляет 1*95/100=0,95 литра или 950 миллилитров, а объем воды 1*5/100=0,05 литра или 50 миллилитров. То есть от всего объема 0, 95 составляет спирт. Чтобы найти процент содержания спирта, нужно объем спирта разделить на весь объема и умножить на 100 (для перевода в проценты). Тогда получим 0,95/1*100=95%). 

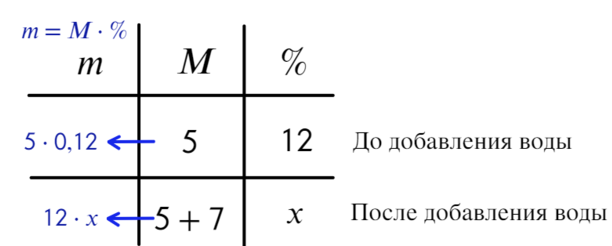
   6      5 * 12 / 100 - объем некоторого вещества. После добавления воды, объем нашего вещества не изменится. А вот объем всего водного раствора составит в итоге 12 литров.

Ответ: 5%.

Задачи с подсказками для закрепления.

Будь в курсе новых статеек, видео и легкого математического юмора.